Pruned RNN-T Explained

This blog explains the paper- ``Pruned RNN-T for fast, memory-efficient ASR training''

Paper theme

RNN-T has a slow and memory-intensive loss function, limiting its use for large vocabularies like Chinese characters. The main idea of Pruned RNN-T is to reduce computational and memory requirements by selectively evaluating the joiner network, leading to faster training and maintained accuracy. Pruning bounds are obtained using a linear joiner network in the encoder and decoder embeddings.

Source Code

Introduction

• Three popular E2E models are CTC models, attention-based models, and RNN-T models, with RNN-T being suitable for streaming decoding and doesn’t assume frames are independent,

• The output of an RNN-T model is a 4-D tensor (\(N\), \(T\), \(U\), \(V\))
  • \(N\) : batch size
  • \(T\) : output length
  • \(U\) : prediction length
  • \(V\) : vocabulary size, which consumes a lot of memory.
• Removing padding, function merging and half-precision training are approaches to reduce memory usage in RNN-T
• In this paper RNN-T = RNN-T loss = transducer loss
• The paper uses a Conformer encoder and a stateless decoder in their experiments, not a recurrent encoder and decoder.

Motivations

Illustration of a generic transducer model. Reference (Lugosch, 2020)

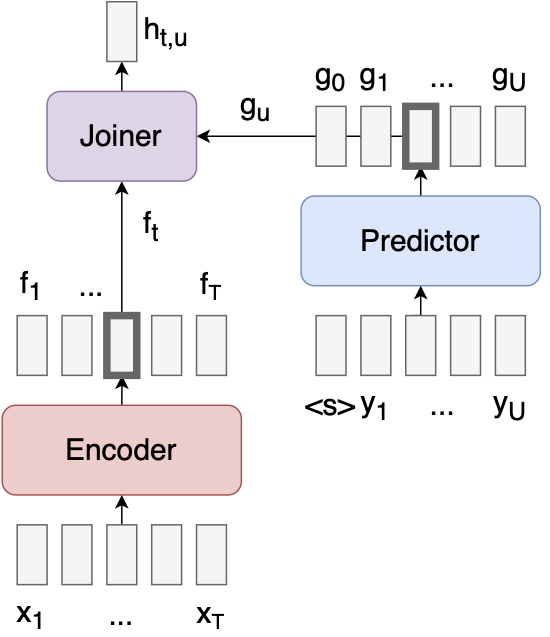
Tokens:

• The transducer model utilizes tokens, such as the Beginning-Of-Sequence (BOS) token <s> placed at y0, and a blank token (∅). It has no EOS.

Equations:

• Input Features:
  • Denoted as: \(\mathbf{x} = \{x_0, x_1, x_2, \ldots, x_{t-1}\} \equiv X_{(T, E)}\)
  • These represent the input features, typically derived from audio or text data.
• Tokenized Transcript:
  • Denoted as: \(\mathbf{y} = \{y_0, y_1, y_2, \ldots, y_u\}\) (with a total of \(U\) tokens)
  • Represents the tokenized transcript, where each \(y_i\) corresponds to a token in the output sequence.
• Predictor Network (Decoder):
  • The predictor network, or decoder, is autoregressive. It takes the previous output as input and generates features used for generating the next output token.
• RNN-T loss computation can be memory and compute-intensive due to the large output shape: \(N \times T \times U \times V\).

This illustration shows the lattice in standard RNN-T (right) vs pruned RNN-T (left). arXiv (Fangjun Kuang, 2022)

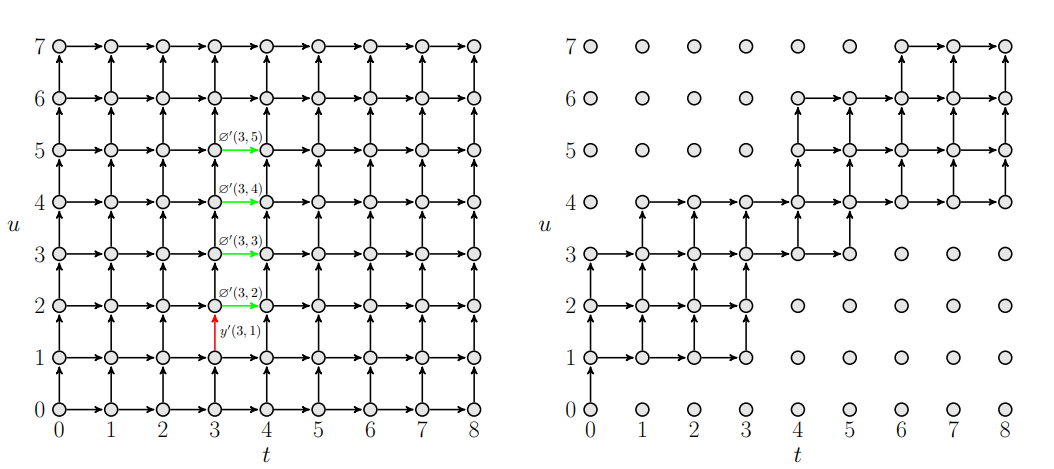
What is a lattice? and why is it important?

The lattice represents the log-probs of transition between the time steps and label indices. They are important because they capture the likelihood of transition to a token at a time step.

• Pruned RNN-T limits the token range from \(U\) to \(S\) at each time step, reducing output shape to \((T, S, V)\). This reduction reduces memory consumption and speeds up training.

Pruned RNN-T

• Pruned RNN-T selectively evaluates the joiner network for specific $(t, u)$ pairs that have a significant impact on the final loss. This is achieved by performing the core recursion of the model twice:
  • First, with a “trivial” joiner network, which is fast to evaluate, to identify important pairs.
  • Then, the full joiner network is evaluated only for a subset of (t, u) pairs.

• Trivial joiner network: The trivial joiner network is a simplified approach to computing the joiner network in the RNN-T model, using matrix multiplication and lookups to efficiently obtain log probabilities for the pruned RNN-T model. \(y(t,u) \rightarrow \text{log-probs of vertical transition}\)
  \(\phi(t,u) \rightarrow \text{log-probs of horizontal transition}\)
  \(L_{enc}(t,u) \rightarrow \text{unnormalized log-probs associated with encoder}\)
  \(L_{dec}(t,u) \rightarrow \text{unnormalized log-probs associated with decoder aka. prediction network}\)
  

  Log probs associated with the joiner is given by

  \[L_{trivial} = L_{enc} + L_{dec} - \log \left( \sum \exp({L_{enc} + L_{dec}}) \right)\]

  this equation allows us to compute \(y(t,u)\) and \(\phi(t,u)\)

• Pruning bounds: Pruning involves selecting a constant \(S\) (eg 4 or 5) to limit the evaluation of \(L(t, u, v)\) for specific \(u\) indexes within a given \(t\) index. In the above illustration, the lattice on the right will have \(L(t,u,v)\) computed for only for \(p_t \leq u < p_t + S\) indices, while the rest is set to \(-\infty\). To compute the globally optimal pruning bounds we want to find a sequence of integer pruning bounds \(p=p_0, p_t, ... p_{T-1}\) that maximizes the total retained probability. It is basically finding positions for pruning in the lattice such that the total probability of retained transition is maximized. Here we are trying to retain the highest probability transition while discarding the less relevant ones.

In the context of the pruned RNN-T model, the quantities \(y′(t, u)\) and \(\phi′(t, u)\) represent “occupation counts” within a specific interval, indicating the likelihood of upward and rightward transitions. Lets estimate the retained probability mass for \(S=4\) (no. of label indices to be evaluated at each time step \(t\)) and \(p_t=2\) (pruning bound)–

\[\phi'(t,2) + \phi'(t,3) + \phi'(t,4) + \phi'(t,5) - y'(t,1)\]

The occupation count \(y'\) in the above equation represents the probability associated with label index 1 which is red in the above lattice diagram. The subtraction is done to make the calculation more accurate by compensating for the inclusion of some probability mass that should have been pruned out due to lower \(u\) values.

• Loss function: Source Code The loss function is a combination of log-probs from trivial joiner network and full joiner network.

\[L_{smoothed} = (1- \alpha^{lm} - \alpha^{acoustic})L_{trivial} + \alpha^{lm}L_{lm} + \alpha^{acoustic}L_{lm}\]

Refer to Section 3.3 in the paper for a more detailed explanation

Experimental Settings

Category	Parameter/Hyperparameter	Value
Dataset	Corpus	LibriSpeech
	Training Hours	960 hours
	Test Sets	test-clean, test-other
	Test Set Speech Duration	Approximately 5 hours each
Input Features	Feature Type	80-dimension log Mel filter bank
	Window Size	25 ms
	Window Shift	10 ms
Data Augmentation	SpecAugment Factors	0.9 and 1.1
Model Architecture	Encoder	Conformer with 12 layers
	Encoder Self-Attention	8 heads
	Encoder Attention Dim	512
	Encoder Feed-Forward Dim	2048
Decoder	Stateless decoder with embedding layer and 1-D convolutional layer
	Decoder Embedding Dim	512
GPUs	Number of GPUs	8 NVIDIA V100 32GB GPUs
Training Strategy	Pruning Strategy	Enable pruned loss after convergence of trivial loss

Results

• Pruned RNN-T outperforms other implementations in terms of speed and memory efficiency.
• When comparing Word Error Rates (WERs) on the LibriSpeech test-clean and test-other datasets, the model trained with pruned RNN-T shows slightly better WER performance compared to the model trained with unpruned RNN-T loss. This suggests that pruned RNN-T can achieve comparable or better accuracy in ASR tasks.

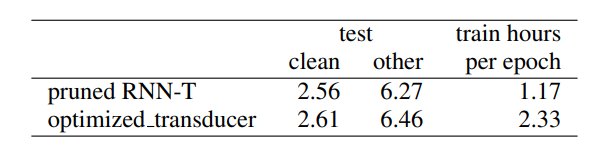
• The memory efficiency of pruned RNN-T allows for the use of larger batch sizes and vocabulary sizes during training, which further contributes to its speed advantage.